Homework #15
Steps To Solving a Linear Programming Problem:
- Based on given constraints, write inequalities
- Graph these inequalities
- Identify the feasible region and vertices of the feasible region on the graph
- Based on the given information, write a profit equation
- Plug the vertices into the profit equation. The maximum and minimum profits are the largest and smallest numbers achieved by plugging in each vertex.
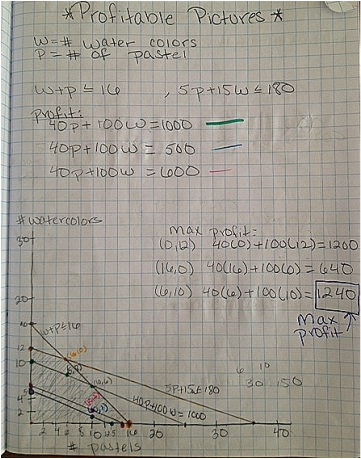
This activity helped me understand the particular steps to solve a linear inequality. The problem gave me information about the cost and profit of each type of painting, his budget for supplies, and that he could make at most 16 paintings. From that I created the two constraint inequalities and one profit equation. The problem asked me to find the maximum amount of money he can make given these constraints. I decided to graph the inequalities on the same plane. I then shaded the feasible region. This feasible region represented the possible combinations of number of water colors and numbers of pastel paintings he could make. Since I know that one of the vertices of the feasible region will yield the maximum profit I plugged each vertex into the profit equation. The vertex (6,10) gave the maximum profit of $1240. After doing this activity I understood that it is important to understand the given constraints because if you do not write inequalities that accurately represent them, then the feasible region will be wrong.
The Big U
The Big U